📄Publications
1. High Reconstructability of Degree-Heterogeneous Networks
J.-J Qin, G Yan. Physical Review Letters, 2025, 134(13): 137402. (Editors’ Suggestion & Featured in Physics)
Abstract: Reconstructing complex networks from observed, often noisy data is a fundamental task crucial for understanding complex systems across various domains. Despite numerous methods proposed for network reconstruction, little attention has been given to the relationship between reconstructability and the intrinsic properties of hidden networks. Here, we present a mathematical proof that, for scale-free networks, the reconstruction accuracy increases as the exponent of the power-law degree distribution decreases. This suggests that degree heterogeneity contributes to higher reconstructability. We validate this conclusion in empirical networks, where nodal degrees may not strictly adhere to power laws. Our results demonstrate that the reconstruction accuracy of degree-heterogeneous networks is indeed significantly higher than that of their randomized counterparts.
synopsis: The Reconstructability of Networks
The fidelity of a complex system’s representation as a network model depends on the diversity of its interconnections.
2. Statistical inference of multi-state transition model for longitudinal data with measurement error and heterogeneity
J.-J Qin, J Guan. Communications in Statistics - Theory and Methods, 2024, 53(20), 7453–7476.
Abstract: Multi-state transition model is typically used to analyze longitudinal data in medicine and sociology. Moreover, variables in longitudinal studies usually are error-prone, and random effects are heterogeneous, which will result in biased estimates of the interest parameters. This article is intended to estimate the parameters of the multi-state transition model for longitudinal data with measurement error and heterogeneous random effects and further consider the covariate related to the covariance matrix of random effects is also error-prone when the covariate in the transition model is error-prone. We model the covariance matrix of random effects through the modified Cholesky decomposition and propose a pseudo-likelihood method based on the Monte Carlo expectation-maximization algorithm and the Bayesian method based on Markov Chain Monte Carlo to infer and calculate the whole estimates. Meanwhile, we obtain the asymptotic properties and evaluate the finite sample performance of the proposed method by simulation, which is well in terms of Bias, RMSE, and coverage rate of confidence intervals. In addition, we apply the proposed method to the MFUS data.
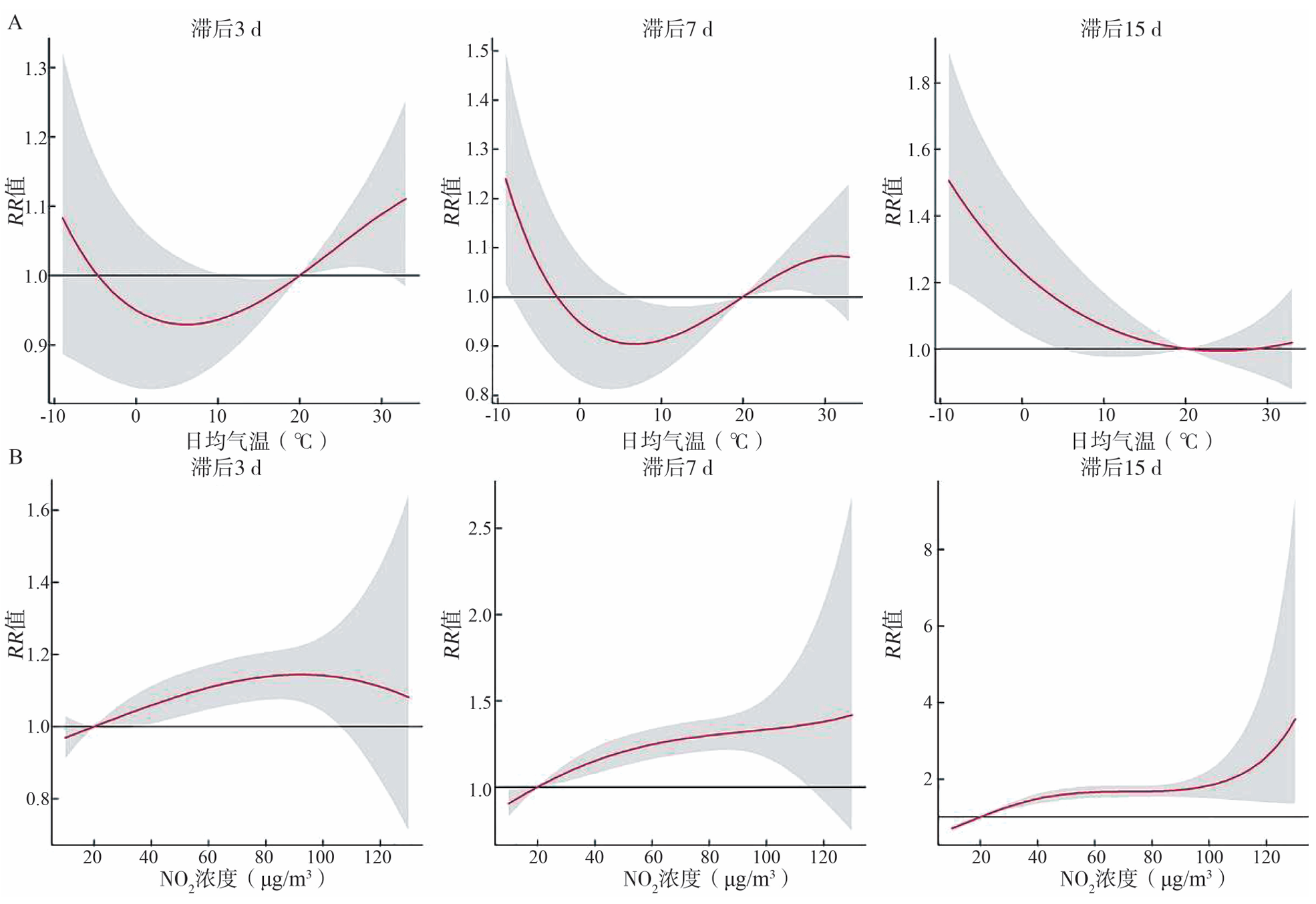
3. Prediction for the outpatient amount of childhood common respiratory diseases based on multivariate LSTM model with lag effect
J.-J Qin, C. Chen, J. Guan, W. Liu. CHINESE JOURNAL OF DISEASE CONTROL & PREVENTION (in chinese:中华疾病控制杂志), 2022, 26(9): 1057-1064.
Abstract: Objective To construct the prediction model of the daily outpatient amount of childhood common respiratory diseases and analyze the trend of the outpatient amount in the future, which will provide data support for the scientific prevention and control of common respiratory diseases in children. Methods Based on the daily outpatient cases of a hospital and meteorological and air pollutant data from January 1, 2017 to December 31 2019, the distributed lag nonlinear model (DLNM) was used to analyze the influence and lag effect of average daily temperature and pollutant concentration on the daily outpatient amount in spring and autumn semesters.A multivariate long and short-term memory (LSTM) model was constructed to predict daily outpatient amounts in the spring and autumn semesters. Results The median average daily temperature in the spring and autumn semesters was selected for research, and we found that the impact of average daily temperature on the daily outpatient amount in the autumn semester lagged 7 days and lasted for about 10 days, while the effect on the spring semester was immediate and lasted for about 4 days.The multivariate LSTM model combined with the lag effect can predict daily outpatient amount in spring and autumn semesters well, the mean absolute percentage error (MAPE) on the test set was 4.59% and 4.77%, respectively. Conclusion The multivariate LSTM model combined with the lag effect can accurately predict the daily outpatient amount, which provides a scientific basis for the prevention and control of diseases.